産業技術総合研究所の一杉裕志氏のサイトで 氏は大脳皮質の計算論的モデル BESOM を提案しています。 それは4つの機械学習技術(自己組織化マップ、ベイジアンネット、独立成分分析、強化学習)を 組み合わせたもので、 すでにプログラムがありソースコードも公開されています。 その機能はもちろんまだ実際の人間の脳の機能からは程遠いとはいえ、 ここまで具体的な脳のモデルを既知の技術の組み合わせにより提示できるということが、 機械学習の進歩を物語っていると思います。
実際の脳にできることを考えてみると、脳の機能をコンピューター上で実現しようとするときの必要条件が見えてきます。
例えば
- ニューロンの活動(化学的な反応)の遅さにも関わらす 高速な処理が可能 → 大規模な並列計算が必要
- 人間の赤ん坊はさまざまな映像の中から一塊の物体や親の顔を認識するようになる → 独立成分分析のような「抽象化」をおこなう仕組みが必要
- 快を求め不快を避けるという動物に共通した性質を実現するには強化学習のような 「報酬」という概念を含む機構が必要
ここで思考実験として、脳のコネクショニスト(つまりニューラル・ネットを用いた)モデルを 人間の脳が持つ能力から逆算しながら構成するということを試みたいと思います。 つまり、知能の個体発生(認知の発達過程)をたどりながら、人間の脳が備えている能力と、 それをニューラル・ネットの手法によって実現する方法を考えていきます。
分節・抽象化
人間の赤ん坊は生れたときは目が悪く、明暗しか分かりません。 遠近の違いや立体なども認識することができません。 それが、いろいろな物や景色を見る体験を通して、形が認識できるようになってきます。 つまり物の形を周囲から切り離して(分節して)認識できるようになるわけです。
また、2ヶ月を過ぎたころからパパとママに対して別の反応をするようにもなります。 つまり、パパの顔の映像を、心の中にある「パパ」という観念に結び付けて認識することができるようになるわけです。 これは、時によって見え方が異なるパパの顔の映像から「パパ」という観念を抽象する操作とも言えます。
パワン・シンハは TED での講演 の中で、生まれつき目の見えない子供たちに視力回復治療をおこなうプロジェクトについて話しています。 子供たちは手術によって外部からの光の情報を網膜を通して受け取れるようになりますが、それだけでは 実世界の物を認識できるようにはなりません。彼らには世界が色や明るさの違う無数の細かい領域に分かれている ように見えていて、例えばボールの影の部分が一つの物として見えてしまうし、四角と丸が重なった図形を 見せると三つの物があると答える。 しかし数ヶ月たつと、丸を丸、四角を四角として、そして現実世界にある物(人、牛、……)を それぞれ一つの物として認識できるようになる。これは、それらの物が一つのまとまりとして動く様を 何度も見ることによって、脳が正しい分節を学習することによります。
分節と抽象化は情報の圧縮という点で一つにくくることができます。現実によく出現するまとまりが一つの 物として扱われるよううまく分節すると、あらゆる現実のパターンを効率よく表現することができます。 また、分節化された個々のまとまりにコンパクトな表現(例えばベクトル表現など)を与え、 高次の処理をおこなうときのための記号とすることが抽象化です。
ここでは autoencoder を使ってこの情報の圧縮をモデル化します。 autoencoder を使えば、情報の圧縮を教師なしで、また SGD と組み合わせてオンラインでおこなうことができます。
知覚による入力 $x$ を受けて、その「表現」あるいは「表象」(representation)を返す関数 A を 「抽象器(Abstractor)」と呼ぶことにします。
また、その逆方向の関数 $\mathrm{A’}$ を一つ固定しておきます。
分節・抽象化の学習は、いろいろな入力 $x$ に対し、$x’=\mathrm{A’}(\mathrm{A}(x))$ として $ ||x-x’|| $ が小さくなる ように $\mathrm{A}, \mathrm{A’}$ を変更していくことに相当します。
運動の学習
やがて赤ん坊は体を動かすことを覚えます。 寝返りさえできない状態から、寝返りし、ハイハイし、立ち上がり、 歩き、ということができるようになっていく過程で、 赤ん坊は体や筋肉をどのように動かすといいのかを学んでいきます。 同時に、口の形を変えたり息を調節したりして音を出すことも学習します。
ある表象 $y$ を受けて「運動」を返す関数 $\mathrm{C}$ を 「具象器(Concretizer)」と呼ぶことにします。
また、ある運動 $z$ をおこなったときに、それに対し、その結果として得られる知覚を 返す関数 $\mathrm{W}$ を「外部世界(World)」と呼ぶことにします。
運動の学習の捉え方はいろいろあると思いますが、ここではこのような場面を想定します。 3ヶ月ぐらいの赤ん坊に親が話しかけると、赤ん坊はそれに反応して片言を発します。 やがて赤ん坊は声を真似するようになり、まず母音が、次に子音が話せるようになり、 8ヶ月ぐらいで「ママ」などと言い始めます。
母親の声を $x$ として、それに対する赤ん坊の頭の中の表象を $y=\mathrm{A}(x)$、 それによる赤ん坊の口の運動を $z=\mathrm{C}(y)$、 それが引き起こす知覚(つまり赤ん坊が聞く自分の声)を $x’=\mathrm{W}(z)$、 それが惹起する表象を $y’=\mathrm{A}(x’)$ とします。
運動の学習は、いろいろな入力 $x$ に対し、$y’=\mathrm{A}(\mathrm{W}(\mathrm{C}(\mathrm{A}(x))))$ として $||y-y’||$ が小さくなる ように $\mathrm{C}$ を変更していくことに相当します。
外部世界モデル
人間は常に今から少しあとに起きることを予想しながら生きています。 例えば道を歩くときも、路面の状態や周りの状況を見ながら一瞬あとを予想し、 それに基づいて次に足を置く位置や歩く速さを調整しています。 人と話しているときには相手の表情や声の調子から一瞬ごとに相手の次の出方を予測し、 それによって次に話す内容や話す調子を決めています。
また、人間は外部からの刺激がなくてもいろいろな状況を自分で想像することがあります。 犬小屋を作る前に頭の中で必要な作業について考えてみたり、 明日会うはずの人に対して、こう言ってみたら何と答えるだろう、などと考えてみたりします。
こういったことから、人間の脳内には外部の世界についてのあるモデルがあると考えられます。 それは大雑把に言えば、人なら誰しも頭の中に持っている、 外部の世界についての「世界とはこんなものだ」とか 「もしこうしたらこうなるだろう」というような考えすべての寄せ集めのことです。
人はいろいろな経験をしながらこの世界についてのモデルを修正していき、 これからの予測のために役立てます。 ジェフ・ホーキンスはその講演の中で、 予測の能力ことが知能の本質だとして重視しています。
ある意志の表象を $y$ として、それに対し、その意志を運動にしたときに 外部世界から返ってくる知覚の予想 $y’$ を返す関数 $\mathrm{W_m}$ を 「外部世界モデル」と呼ぶことにします。
外部世界モデルの学習は、いろいろな意志の表象 $y_1$ に対し、 $ y_1=\mathrm{A}(\mathrm{W}(\mathrm{C}(y))), y_2=\mathrm{W_m}(y) $ としたときに $ ||y_1-y_2|| $ が小さくなる ように $\mathrm{W_m}$ を変更していくことに相当します。
報酬の最大化
快を求め不快を避けるという動物に共通する傾向のモデルとしては強化学習が有名ですが、 ここではあくまでもニューラル・ネットにこだわってみたいと思います。
ある表象 $y$ を、別の表象 $y’$ と「報酬(reward)」$r$ の組に写す関数 $\mathrm{T}$ を「思考器(Thinker)」と呼ぶことにします。
ここで、人間ではある種の知覚(や表象)とある種の情動(例えば恐怖など)が固定的に結びつけられていることを考えると、 $\mathrm{T}$ のパラメターの一部は固定されているのかもしれません。
「思考器」というときの「思考」は広い意味で捉えています。いわゆる「感じる」ことも含まれます。 また、考えるという行為は思考器だけでおこなうのではなく、外部世界モデルも使います。 思考器と外部世界モデルの間を表象がいったりきたりすることで考える、ということをイメージしています。 考えるためのモジュールから外部世界モデルだけを切り離したのは、そこだけで別に学習できるのでは、と思ったからです。
一方で、思考という行為の複雑さから考えると、$\mathrm{T}$ はそれ自体の中にループを含む、 recurrent なネットワークになっているのかもしれません。
思考器の学習は、いろいろな表象入力 $y$ に対し、 $(y’, r) = \mathrm{T}(y)$ で得られる報酬 $r$ を大きくするように $\mathrm{T}$ を変更していくことに相当します。
また、報酬を最大化するための更新は $\mathrm{T}$ にとどまらず $\mathrm{W_m}$ に対してもおこなわれる、と考えることもできます。
これをまとめると以下の図のようになります。
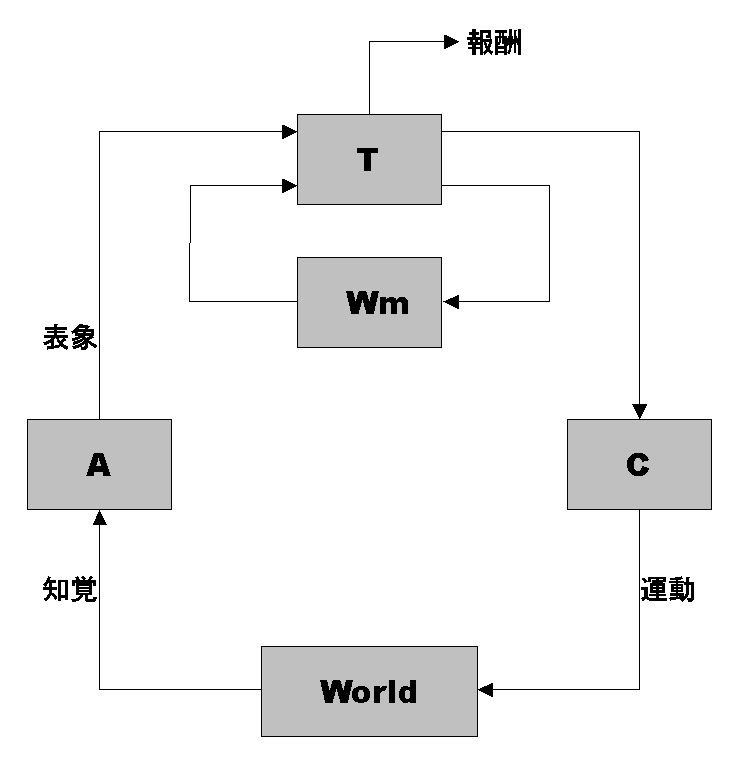
$\mathrm{T}$ は初期状態では恒等写像とします。
モジュールの更新はだいたい $\mathrm{A}, \mathrm{C}, \mathrm{W_m}, \mathrm{T}$ の順番でおこないますが、厳密ではありません。 赤ん坊は外部世界について学習しながら運動することも同時に学びます。 大人になってから外国語を学ぶとき、聞き取りない音が聞き取れるようになるには $\mathrm{A}$ の再学習が必要になりますし、また話すためには $\mathrm{C}$ が更新されるはずです。 また、一般に思考器と外部世界モデルはお互いに影響し合いながら同時に更新されていくでしょう。 もちろん大人よりも子供や赤ん坊の方がより学習が強くおこなわれ、柔軟に周囲の環境に適応 することができるのは確かです。
本能のような最初から固定されている部分、 ある年齢まではさかんに学習をおこなうがそれ以降はあまり更新されない部分、 などの違いを可能にするためには、学習の強さやその時間的な制限条件を決める追加のパラメターが必要となるでしょう。
このモデルでは、人間は外部世界と合わせて一つの recurrent なネットワークを形成しています。 知覚した情報を分節化することを学びながら運動することを学習し、 外部世界についての考えを深めながら自己実現(報酬の最大化)を学ぶ、というように、 このネットワークはさまざまな刺激を得ながら各モジュールを同時に更新していきます。 この EM 的な更新と recurrent 性により、遠い因果関係をたどったり、はるか未来に受け取るはずの報酬を最大化するなど、 各モジュールにおいて複雑な関数を学習できる可能性があります。